LaTeX templates and examples — Math
Recent

A custom .sty and template for college math homework.

A very quick and easy to understand introduction to Gram-Schmidt Orthogonalization (Orthonormalization) and how to obtain QR decomposition of a matrix using it.

A final assignment for measurement and error propagation in a sophomore physics lab course.

Göteborg universitet, Chalmers universitet

Le modèle linéaire mixte a été mis en oeuvre dès les années 1950, essentiellement dans le domaine de la génétique animale (réf. Henderson[1],[2]). Il n’a toutefois connu une utilisation plus générale qu’au cours des années 1990, en relation avec le développement de nouvelles procédures de calcul dans le cadre des logiciels statistiques. L’utilisation du modèle linéaire mixte soulève, par rapport aux modèles classiques d’analyse de la variance, un certain nombre de difficultés particulières, tant en ce qui concerne l’estimation des différents paramètres que la réalisation des tests d’hypothèses. Des informations peuvent être trouvées à ce sujet dans les articles de Littell [2002], McLean et al. [1991], et Piepho et al. [2003], et dans les livres de Demidenko [2004], McCulloch et Searle [2001],

Fundamentos Matemáticos para Computação 1 - 2015.2 - IMD Avaliação 2: Teoria dos Números, Congruência Autor: Patrick Terrematte
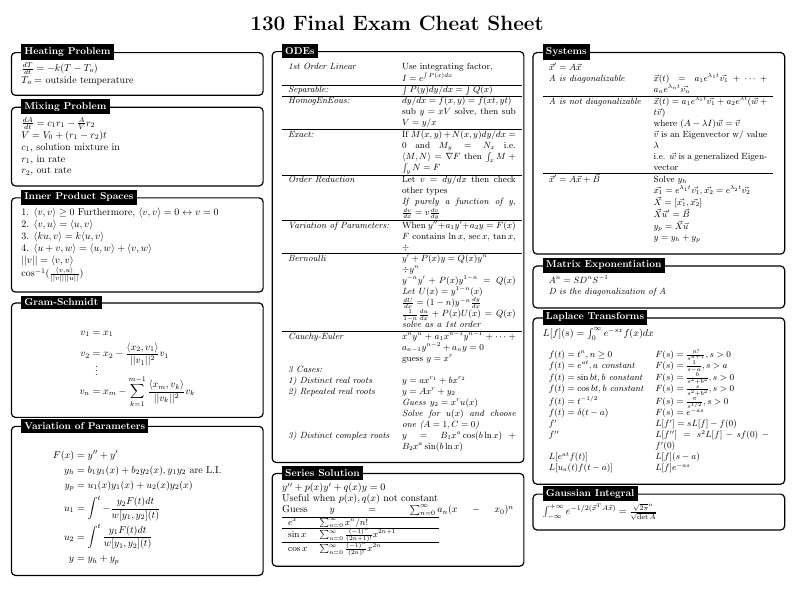
Cheat sheet for Linear Algebra and Differential Equations

Math homework for Accelerated Math students in Howard County, Critical Thinking Questions.

homework 8w
\begin
Discover why over 25 million people worldwide trust Overleaf with their work.